“Neexistuje. Ztroskotali na ní největší géniové této planety”, tvrdí “věhlasný” německý profesor matematiky Albrecht Beutelspacher. Nalezení této rovnice jsem zadal svým studentům jako semestrální práci. Neztroskotal nikdo.
(poprvé publikováno 20. 4. 2018)
Ředitel “věhlasného matematického muzea” v německém Giessenu, “věhlasný profesor” Albrecht Beutelspacher, hlásá neuvěřitelné matematické bludy. Alespoň tedy podle serveru Novinky.cz. Před časem jsem si zde přečetl článek s názvem Matematikům se stále nedaří definovat tvar vejce – viz
http://www.novinky.cz/veda-skoly/297571-matematikum-se-stale-nedari-definovat-tvar-vejce.html
“Věhlasný profesor” tvrdí: “Je jen jeden kruh – velký, nebo malý, jeden čtverec – velký, nebo malý, ale různá vejce. Některá jsou podlouhlejší, jiná téměř kulovitá. I kdyby tu byl dokonalý vzorec pro jeden tvar vajíčka, nebyl by to vzorec pro všechna vejce.”
Matematické myšlení tohoto člověka zjevně uvízlo někde ve starověku. V Německu možná stačí na profesuru nějaké věhlasné německé univerzity. U nás by nejspíš způsobilo nedostatečnou v prvním ročníku gymnázia.
Soudnému člověku se nechce věřit, že by profesor matematiky používal argumentaci na úrovni žáčka základní školy. Už středoškolák by totiž měl vědět, že třeba i elipsy jsou takto „různé“. Ani elipsa totiž není jen velká, anebo malá. I elipsy jsou některé protáhlejší, některé téměř kulaté a některé jsou kulaté dokonce úplně. Přesto existují dokonalé „vzorce“ pro všechny elipsy. Jeden z nich je např.
x=a.cost
y=b.sint
Ty „podlouhlé“ mají třeba a=10;b=1; ty „kulatější“ a=8;b=7; ty úplně kulaté se nazývají kružnice a mají například a=8;b=8.
V článku se například dočteme, že na vejčitém tvaru ztroskotali i největší géniové. Jediný, kdo prý tvrdil, že vejčitý tvar objevil, byl Albrecht Dürer na přelomu 15. a 16. století. Ale prý to „nebyla perfektní forma vajíčka, ale elipsa“ (autor článku měl zřejmě na mysli elipsoid).
Že na vzorec vejčité plochy (ovoidu) nepřišel Albrecht Dürer, to bych mu nevyčítal. Dnes už je ale věda přece jen trochu dál. Dnes existuje jediný vzorec i pro tak rozdílné tvary, jako je tovární komín, špička tužky a karoserie auta. Jakého – to je jedno, vyberte si, jaké chcete. Dnes už umíme jediným vzorcem popsat tak rozdílné a složité tvary, jako je turbína v elektrárně, křídlo letadla a trup lodě. Ví to každý student prvního ročníku technické vysoké školy (alespoň tedy té naší). A studenti některých našich speciálních oborů by měli být schopni u jednoduchých tvarů ty rovnice i napsat.
Článek mě inspiroval k tomu, že jsem dvěma skupinám svých studentů druhého ročníku oboru Matematické inženýrství zadal semestrální práci tohoto znění:
Definujte ovoid (plochu „vejčitého tvaru“) a uveďte jeho obecnou rovnici. Tuto obecnou rovnici ověřte na konkrétních vejcích různých „tvarů“ – slepice, papoušek, pštros, alka. Napište program, který bude ovoid dle zadané rovnice sestrojovat.
Netroufal bych si tvrdit, že všichni moji studenti jsou chytřejší než největší géniové. Faktem však zůstává, že neztroskotal nikdo. Na “různý tvar” a “různou velikost” elipsy byly potřeba dva parametry (velikosti poloos). U ovoidu jsou potřeba parametry čtyři. Rovnice bude, pravda, trochu složitější, ale to je asi tak všechno, v čem se tyto dvě situace liší.
Plochu “vejčitého tvaru” můžeme definovat například takto: Ovoid je každá plocha, která má rovnici
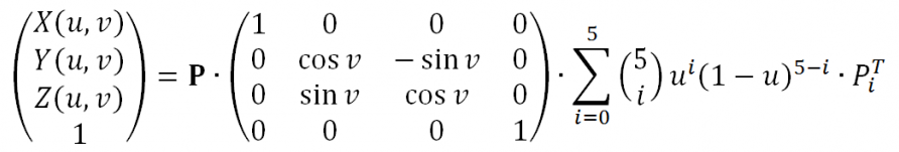
kde P je regulární matice libovolného podobného zobrazení, P0;..;P5 jsou body projektivního prostoru o souřadnicích P0=(0;0;0;1); P1=(0;a;0;1); P2=(1;b;0;1); P3=(2;c;0;1); P4=(3;d;0;1); P5=(3;0;0;1); 0<a<b<c<3; 0<d.
Rovnice vypadá na první pohled složitě, ale čtenář znalý základů počítačové geometrie určitě v sumě poznává Bézierovu křivku pátého stupně, která pro zadané řídicí body vypadá nějak takto:
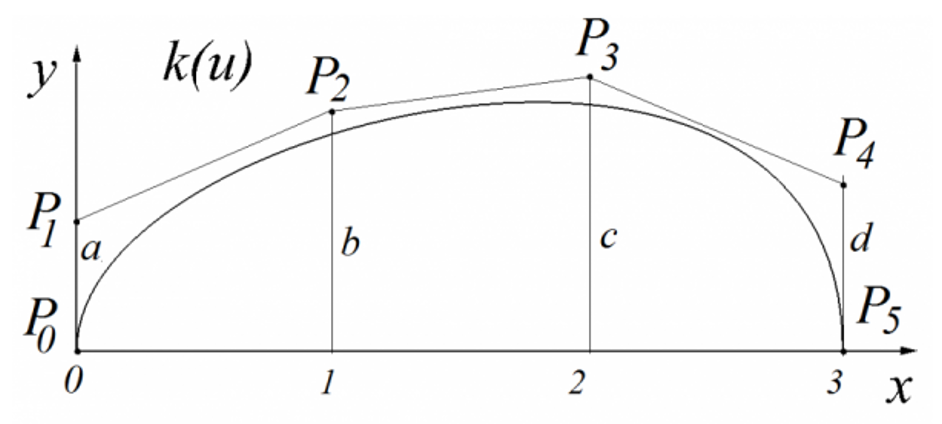
a každý matematik zřejmě vidí matici rotace kolem osy x. Definovaný tvar tak vzniká rotací této křivky kolem osy x:
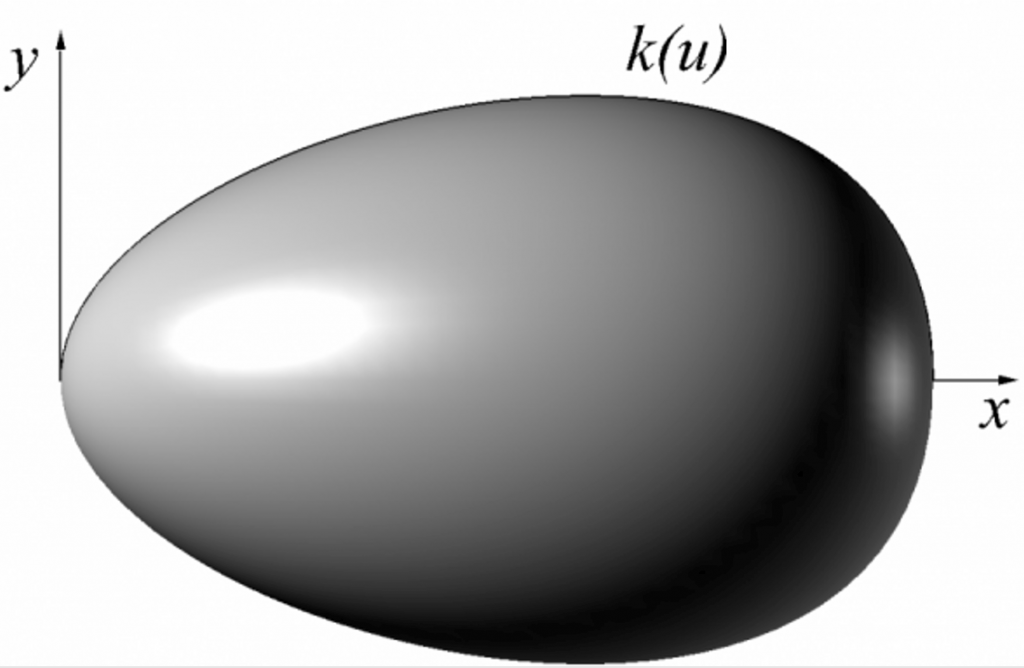
Různou volbou parametrů a, b, c, d pak dostaneme vejce podlouhlá

téměř kulatá

téměř špičatá

či jakákoliv jiná. A třeba i vejce konkrétních ptáků.
Alka
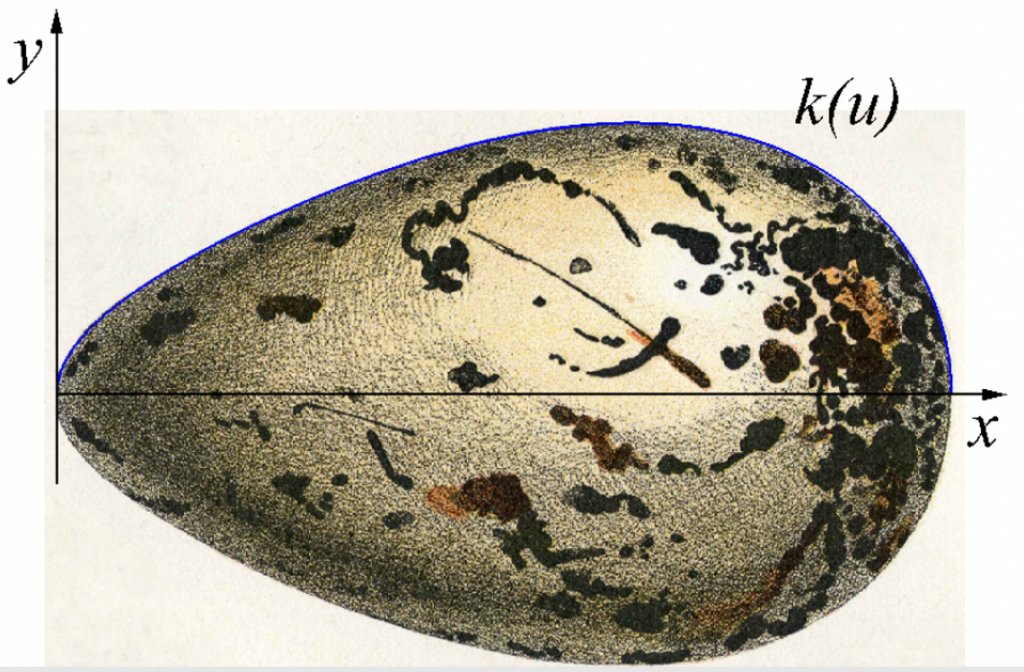

papoušek


pštros


a nakonec i ta slepice

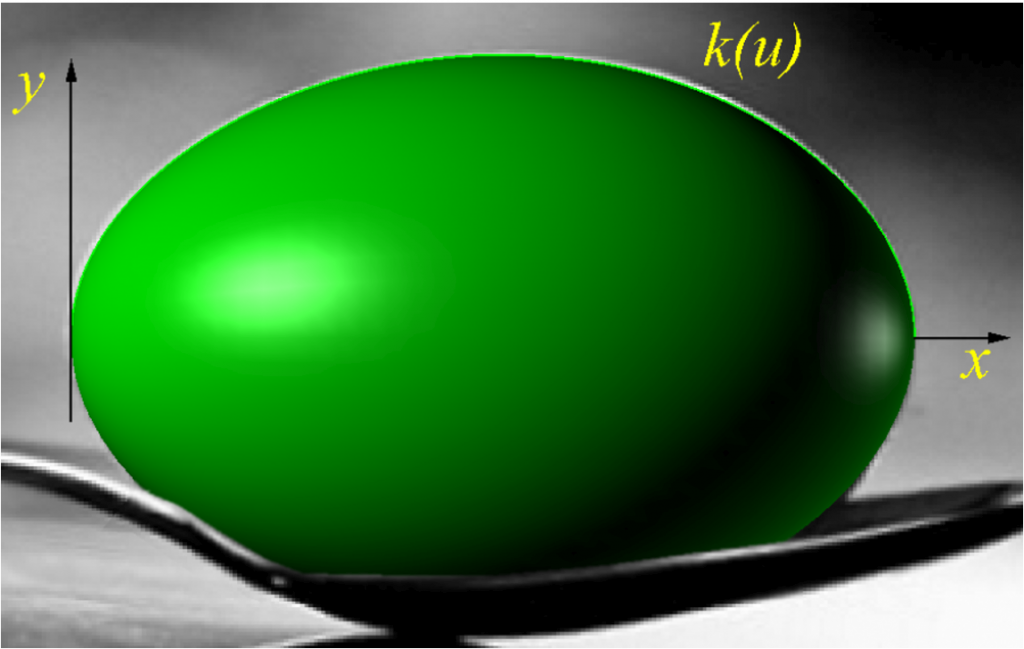
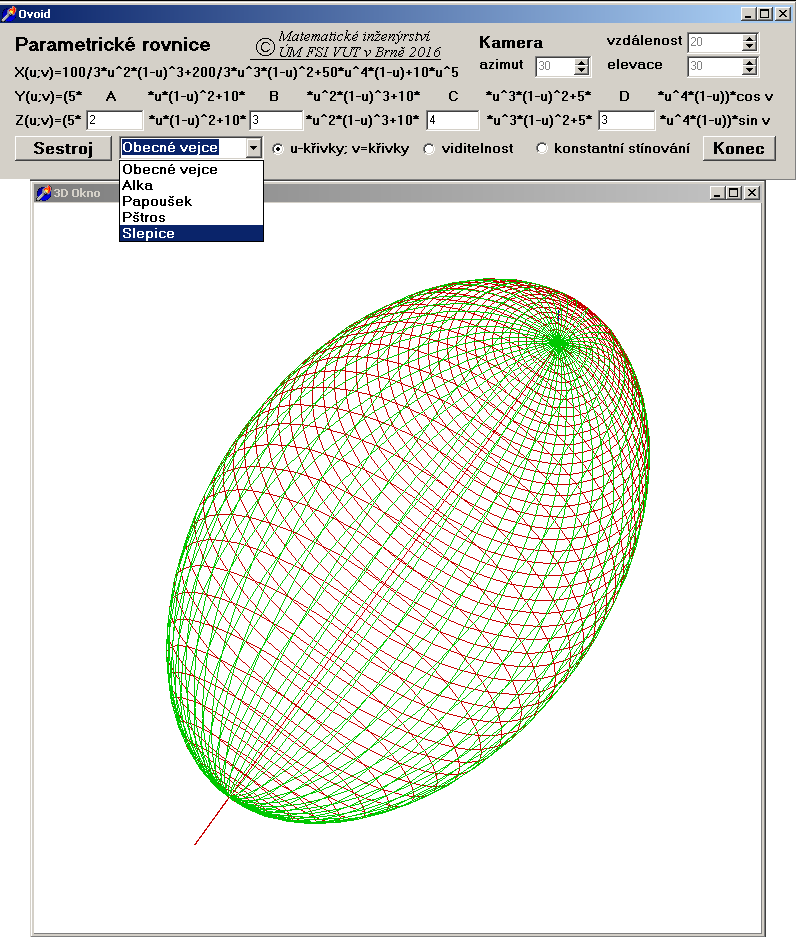
V Giessenu by se měli zamyslet nad tím, zda celá německá matematika i s jejich věhlasnými profesory a řediteli nepatří do nějakého muzea…