Víte, co je to délka úsečky? Nepochybně ano. Přesto vřele doporučuji, abyste si přečetli “vědecký článek” o tomto pojmu, který vyšel v časopise Učitel matematiky určeném pro učitele základních a středních škol. Věřte, stojí to za to.

Nehodlám tady zmiňovat všechno, co za zmínku stojí, to by bylo opravdu hodně dlouhé čtení. Tak aspoň stručný výběr.
Citovat, citovat, citovat…
Citace se v každém článku vždy vyplatí, a to hned z několika důvodů:
- Citace dodávají každému článku punc vědeckosti. Dnes můžete napsat jakoukoliv pitomost. Jestliže k ní připojíte citaci, zůstane sice pitomostí, ale už pitomostí vědeckou.
- Citovat a převzít do “vědeckého” článku je potřeba každou malůvku. I tu nejjednodušší a chronicky známou. I zde totiž platí bod jedna. Kromě toho autor zakryje smutnou skutečnost, že ani takový piktogram není schopen vytvořit sám…
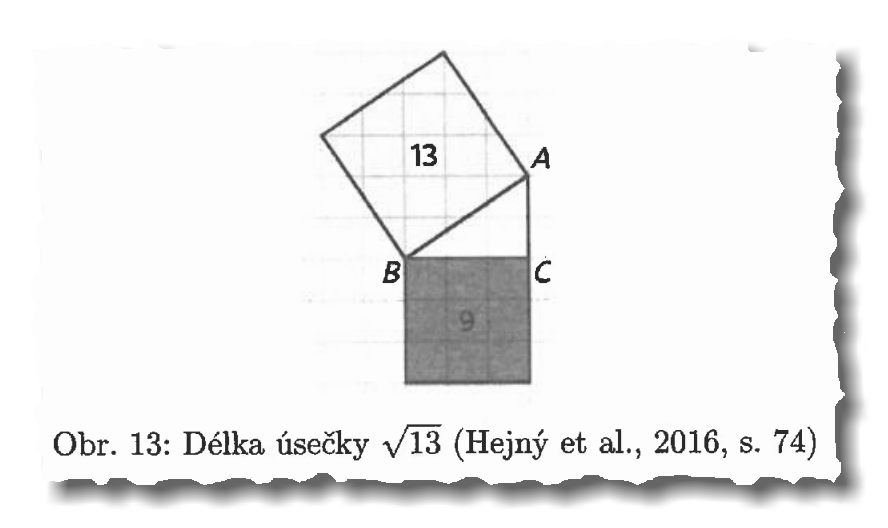
A konečně
3. Je-li i taková trivialita na úrovni šesté obecné náhodou špatně, nemohu za to já, ale v tomto případě Hejný nebo možná někdo z et. al.
Teorie měření včera, dnes a zítra…

Ano, s dnešním měřením délky úsečky tento axiom nemá již nic společného. Zvláště na základní škole. To proto, že žádné dnešní dítě nemusí už Archimedovy úsečky nanášet. Stačí je přiložit, a to všechny najednou. Má je totiž vypáleny v plastu.

Jakpak by to mohlo být v souladu s Eukleidovým pojetím, když Eukleides žádný plast neznal? A bůhví, v čem bude stupnice vypálena za sto let, takže bude s Eukleidem v nesouladu stále větším a větším…
Existující metrika na neexistujících bodech
Znalcům díla Járy Cimrmana je jistě známa basilejská odpověď našeho velikána na otázku, jak mohl neexistující filosof stvořit existující filosofii. Aplikoval jsem Cimrmanovu teorii externismu na definici metrického prostoru, kterou jsem objevil v tomto pozoruhodném článku, a podařilo se mi sestrojit existující komplexní metriku na neexistujících bodech.
Výchozí definice zní takto:

Postrádáte-li v ní jistou drobnost (ovšem co je v matematické definici drobnost, že?), postrádáte správně. A postrádáte-li drobnosti dvě, postrádáte ještě lépe.
O drobnosti číslo jedna autoři článku věděli.
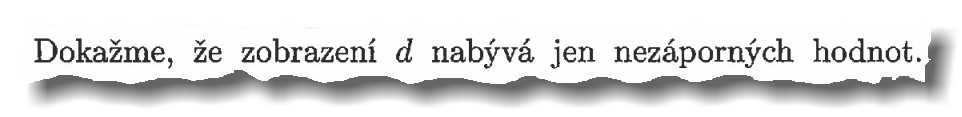
A důkaz tam skutečně je. Kupodivu bez citace. Že by ho vymysleli sami autoři? Možné to je – takto definovaný metrický prostor s exkomunikovanou nezáporností se jen tak nevidí. Je to totiž pověstné škrabání se levou rukou za pravým uchem. Navíc poněkud nedůsledné.
Pokud bych si já takto liboval v rádoby obecných definicích, které bych pak musel dotesávat větami a důkazy, neomezil bych se na reálné hodnoty. Metriku bych definoval jako zobrazení nikoliv do čísel reálných, ale komplexních. Taková úsečka o velikosti 3+2i, to by přece bylo něco!
Jenže pak bych se musel vrátit do reality a dokázat, že metrika nabývá jen reálných hodnot:
Důkaz (sporem):

Teprve teď je možno zaútočit větou o hodnotách nezáporných a teprve až po dalším důkazu se dostat tam, kde bych mohl být přímo a okamžitě, kdybych se nesnažil být za každou cenu originální..
To všechno ovšem ještě není všechno. Zbývá drobnost číslo dvě. Všimněte si, že definice v článku po množině bodů nepožaduje vůbec nic. Připouští tedy i množinu prázdnou. A to je přece úžasné – axiomy pak hovoří o bodech, které neexistují. A jak známo, po neexistujících objektech může matematika zcela korektně požadovat naprosto cokoliv. Tedy i existenci uspořádaného tělesa komplexních čísel. A to je v tomto případě něco úžasného – zobrazení Ø Χ Ø → C, které splňuje tři výše uvedené axiomy, totiž definuje existující komplexní metriku na množině neexistujících bodů…
Jak veliký je bod?
Se samotným závěrem článku ovšem musím bezvýhradně souhlasit:

Ano, je to tak. Já znal jednoho ve Vršovicích, co ztratil brýle. A ten tvrdil, že kocour odnaproti je bod.
Bod může mít dokonce tvar obdélníku o rozměrech 13 cm x 3 cm:

Takže bodu zdar a hodně duševního zdraví…