Opět se objevilo téma, které rezonuje českým školstvím již mnoho let a které se pravidelně opakuje. Matematik by řekl, že je to téma periodické. Následující článek není o tom, co se děje teď, jak by se mohlo zdát podle prvního odstavce. Poprvé jste ho mohli číst před pěti lety. Mnozí asi tuší, proč ho vytahuju právě teď. Teď totiž na toto téma doslova vybuchla bomba…
(poprvé publikováno na blogu iDnes 13. 5. 2015 )
Cermatu se zase něco povedlo. Kvůli jedné maturitní úloze se už opět sepisují znalecké posudky, zasedají hodnoticí komise, vydávají se závěrečné zprávy. A o správnosti matematické úlohy bude možná rozhodovat soud.
O úloze jsem se dověděl z MF DNES dne 12. 5. 2015 a lze ji najít zde. A abyste nemuseli překlikávat stránky, tady ji máte:
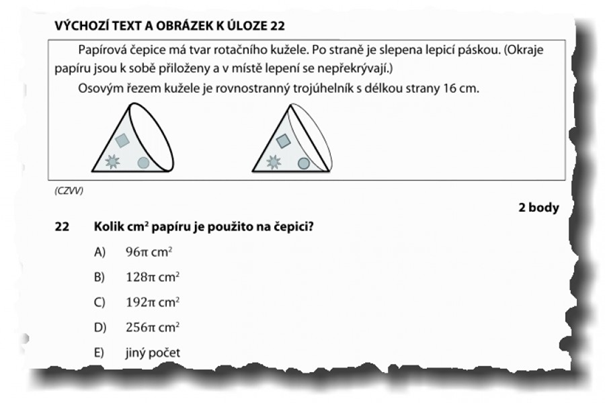
Správná odpověď podle Cermatu je B). Část maturantů se ovšem domáhá odpovědi C). V čem je problém? Odpověď B) je správně v případě, že se do čepice nezapočítá “dno čepice”, odborně řečeno podstava kužele, jehož tvar má čepice mít. Odpověď C) je správně v případě, že toto “dno” započítáno je. Jde tedy o tento otazník

Argument pro odpověď C) je na první pohled zcela absurdní – čepice přece dno mít nemůže, protože by nešla nasadit na hlavu. Věc má ale háček, v tomto případě dokonce velký hák – o tom, zda čepice jde, anebo nejde nasadit na hlavu, není v zadání ani slovo.
Oldřich Botlík ve svém odborném posudku, jehož kompletní znění je k dispozici např. zde, uvádí mimo jiné:
“EDUin mě požádal o stanovisko.., zda je čepice podle zadání tvořena pláštěm rotačního kužele a podstavou, nebo jen pláštěm rotačního kužele bez podstavy… Autor úlohy napsal, že čepice má tvar rotačního kužele. Rotační kužel je plné těleso – podobně jako třeba kulečníková koule nebo obyčejná cihla. Určitě tedy má podstavu – dno čepice.
Autor úlohy dále tvrdí, že osovým řezem kužele je rovnostranný trojúhelník. Jako matematik tedy určitě nemůže mít na mysli čepici bez dna („kornout”), protože třetí ze stran tohoto trojúhelníku (ta, která není součástí pláště) patří do osového řezu jedině tehdy, je-li kužel chápán včetně své podstavy… papírová čepice bez dna odporuje zadání.”
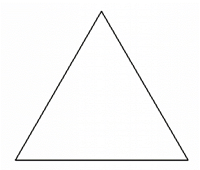
Ano, kolega Botlík má pravdu v tom, že papírová čepice bez dna odporuje zadání. Je tedy určitě pravdě blíž než Cermat. Ovšem mýlí se i on – zadání odporuje nejen papírová čepice bez dna, ale i dutá papírová čepice, která dno má. A správná odpověď není ani B), ani C). Problém je v tom osovém řezu. Podle zadání je to rovnostranný trojúhelník. Ten ale nevypadá takto
ale takto:

Trojúhelník je totiž podle své definice průnikem tří polorovin, takže do něj patří nejen jeho hranice (obvod), ale i všechny jeho vnitřní body. Je-li tedy osovým řezem rovnostranný trojúhelník, jak se píše v zadání, není čepice ani pláštěm kužele (tj. kornoutem bez dna), ani povrchem kužele (tj. kornoutem s dnem). Nejen kužel, ale i čepice sama – tak, jak je zadána – je plným tělesem, podobně jako třeba kulečníková koule nebo obyčejná cihla.
Že si takovou papírovou čepici nedokážete představit? Já docela snadno, a to i na vícero způsobů, např.
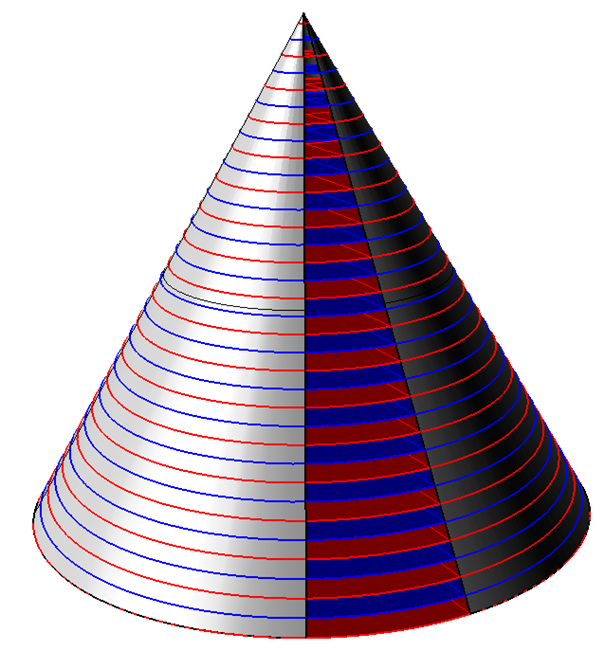
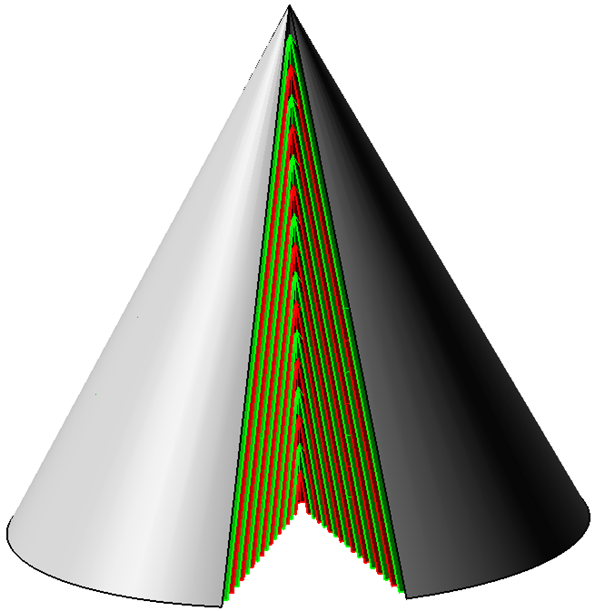
Pravda, aby takto vznikl skutečně přesný kužel, musel by být papír nekonečně tenký. Ale o tloušťce papíru se v zadání nepíše nic, takže taková představa zadání neodporuje. Zajímavější a podstatnější je ovšem to, že nekonečně tenkého papíru bychom na tyto čepice potřebovali nekonečně mnoho. Takže “správnější” než B) i než C) je odpověď E) – jiný počet, i když připouštím, že slovíčko “počet” je v případě nekonečna poněkud nepatřičné.
Už vidím komentáře – přestaň blbnout, zapomeň na ty matematické šílenosti a řiď se zdravým selským rozumem – všichni víme, jak vypadá papírová čepice, takže správně je B). Ovšem každého, kdo mě takto okřikne, se budu ptát: byla to maturita ze “zdravého selského rozumu”, anebo z matematiky?
Podívejme se ještě jednou na ty dva sporné osové řezy:
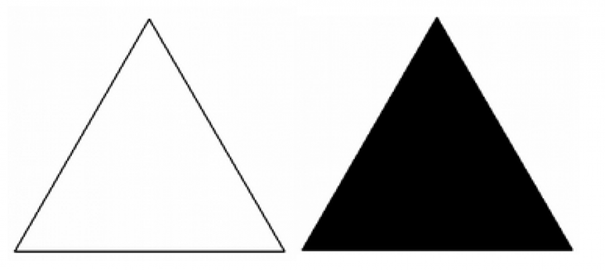
Podle “zdravého selského rozumu” je v tom levém podstatně méně černých bodů než v tom pravém. Každý matematik ovšem řekne, že to není pravda. Podle “zdravého selského rozumu” nemůže jeden elektron projít současně dvěma otvory. Každý fyzik ovšem ví, že může. Podle “zdravého selského rozumu” byla ještě před několika staletími Země plochou deskou, která plave v moři. Dnes už i každý sedlák ví, že tomu tak není.
Dovolte mi tedy poslední matematickou zvrhlost. Podle zadání je čepice prostě kužel – “plné těleso”, podobně jako cihla. Otázkou, kolik je v ní papíru, se tedy ptáme na objem kužele, přičemž tento objem se má udat v centimetrech čtverečných. Každý sedlák ovšem ví, že objem se měří v jednotkách nikoli čtverečných, ale krychlových. Zadání úlohy je tedy logicky sporné. A každý matematik ví, že z logicky sporných předpokladů lze matematicky zcela korektně odvodit naprosto cokoliv. Podíváme-li se tedy na celou věc takto, jsou správně nejen všechny odpovědi, které jsou za úlohou nabídnuty, ale dokonce i všechny ty, které si lze vymyslet a které v nabídce nejsou. Mně osobně tam chybí možnost
F) Cermat měl být už dávno zrušen.
PS: Když jsem to před pěti lety psal, netušil jsem, jaké střelivo mi k tomuto závěru poskytne Cermat letos. O tom zanedlouho v příštím článku.