Časopis Učitel matematiky opět nezklamal. Opět jsem narazil na článek, kde je skoro všechno špatně. Některé chyby jsou dokonce na úrovni základní školy…

Začněme něčím tak ze šesté třídy ZŠ. Může být podíl dvou kladných čísel záporný? Podle autorů článku ano. Pravda – tuto prostou otázku a svoji odpověď trochu zakuklili do poněkud vznešenějších pojmů…

…ale i tak je to látka cca sedmé osmé třídy základní školy. Ypsilon samozřejmě neklesá bez omezení. Nepřímá úměrnost je zdola omezena nulou.
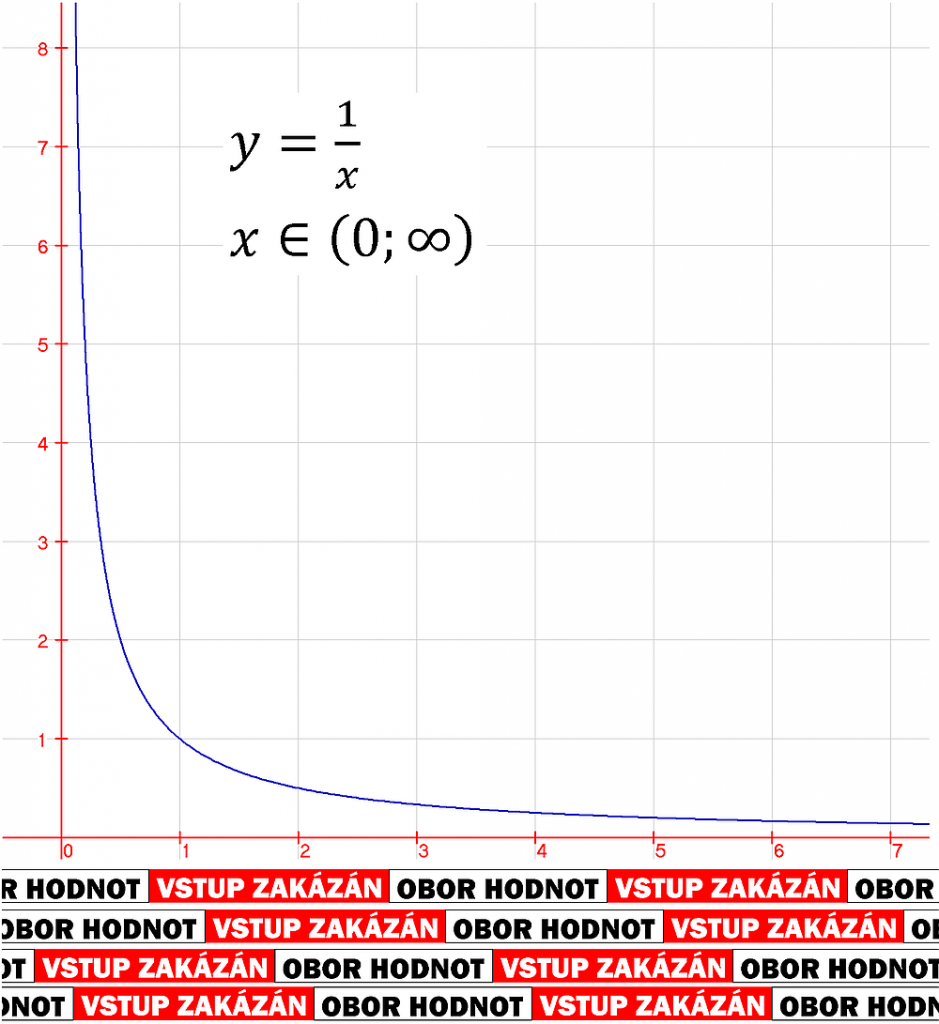
V článku se můžeme dále dočíst:

Takto to prý chápal Eukleidés. Eukleidés zcela přirozeně chápal mnohé věci jinak, než je chápeme dnes. Jestliže jsou ovšem jeho myšlenky prezentovány žákům jako myšlenky současné a dokonce jako alternativa k „obvyklému pojetí“, musím se domnívat, že se díváme na výtvor „moderního“ učitele matematiky – učitele, který „zase až tak moc matematiku umět nemusí“. Právě takoví učitelé jsou schopni korektní definice a přístupy s nádechem opovržení označit za „obvyklé“…

…zatímco oni jsou „neobvyklí“ a tudíž zajímavější.
Jestliže takový „moderní“ učitel bude dnes před třídou prezentovat konkrétně tento příklad, pak podle mého názoru automaticky rozdělí studenty do tří skupin. První, obávám se, že čím dál větší, skupině studentů bude jakékoliv matematické tvrzení úplně jedno. Jedním uchem tam, druhým ven; v lepším případě se to naučí papouškovat. Spokojen bude žák, spokojen bude učitel, a přitom je všechno špatně.
Studenti druhé skupiny takovému učiteli okamžitě stejným způsobem „dokáží“ pravý opak:
Kdo má pravdu? Odpověď je jednoduchá – samozřejmě nikdo, obojí je špatně. A nikdo nebude schopen přijít na to, v čem je chyba. „Moderní“ učitel neovládající matematiku zuří, protože se právě znemožnil a studenti se baví krokem, který právě učinili směrem od matematiky. Ještě pár takových „paradoxů“ a královna věd se pro ně stane alchymií a její učitel komickou figurou.
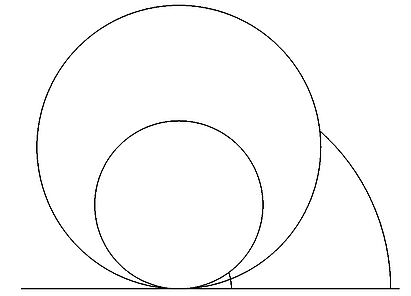
To až student třetí skupiny (bude-li dnes vůbec jaký) se začne ptát: A jaký oblouček vlastně určuje ten „správný“ úhel?
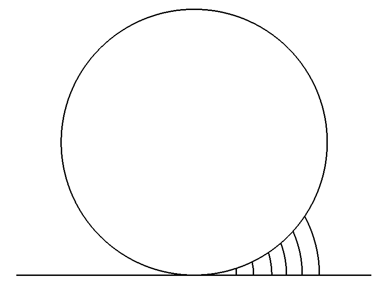
A možná přijde i na to, že žádný. Že je třeba především uvažovat úhel tečny a sečny (kterou jim učitel bůhví proč zatajil), dále sestrojit posloupnost velikostí těchto úhlů pro stále menší obloučky a konečně určit limitu této posloupnosti. Až ta je tou „správnou“ velikostí. A je rovna nule. Nejen pro kružnici s libovolným poloměrem, ale pro každou křivku a každý její bod, pokud v něm tečna existuje. Pro Kuřinu a Vondrovou je to možná příliš obvyklé, fádní a nezajímavé, ale na rozdíl od jejich pseudozajímavého moderního výstřelku je to správně.

Kladná odpověď je špatná odpověď, ale mě už to ani nepřekvapuje. Kartézský součin {1;2}x{1;2} má určitě větší mohutnost než množina {1;2}. A dobře, že to tak je, jinak by nám nefungovala násobilka. Přejděme ale skutečnost, že autoři ve své honbě za originalitou jaksi zapomněli uvést, že kladnou odpověď si zaslouží jen množiny nekonečné, a sledujme dál tok jejich myšlenek:


Vida, tak on ten myšlenkový tok bude tokem někoho jiného. Tento původní Cantorův nápad opsali autoři od Zamarovského, když ho předtím od někoho zřejmě opsal Zamarovský a buhví, kde řetěz opisovačů začíná. Někdo z nich každopádně opisoval špatně. Zamrovského zip

totiž rozbil Richard Dedekind, a to už sto padesát let předtím, než ho Zamarovský(?) vynalezl. A dnes by mu mohli vylomit nějaký ten zoubek i šikovnější studenti. Třeba následujícím protipříkladem:
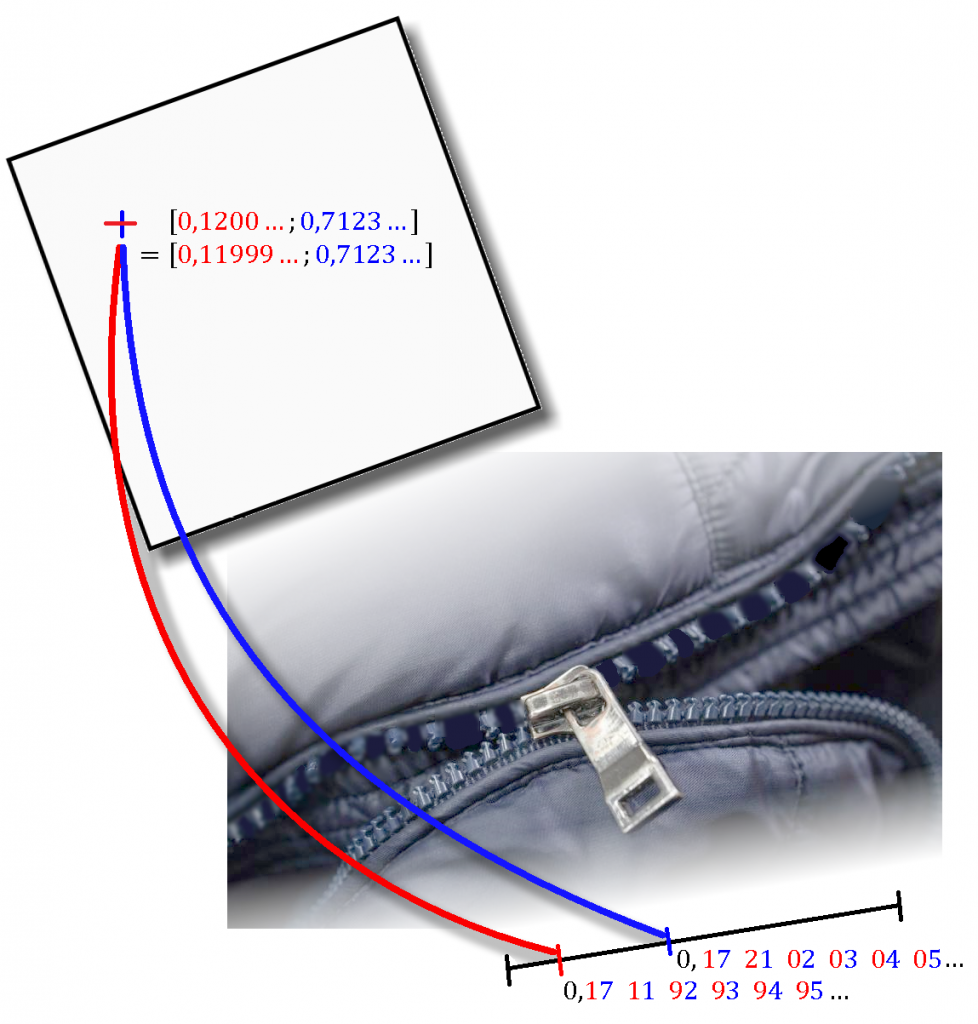
A takto vylomených zubů je na prapodivném zipu nekonečně mnoho. Pro úplnost dodejme, že prosté zobrazení existuje, ale je trochu složitější. Zip na něj rozhodně nestačí.
Článek je vůbec z velké části nekomentovaným přepisem duševních pochodů Petera Zamarovského, který (jen tak mimochodem) není matematik. Tandemu Kuřina & Vondrová to buď nevadilo, anebo to z jeho textu nepoznali. Kdo je čím, to se dnes vůbec poznává dost těžko. Ten umí to a ten zas tohle a všichni dohromady neumíme nic…

Aristoteles byl (spolu s výše jmenovaným Eukleidem) jedním z největších antických myslitelů. Ale používá-li někdo jeho argumenty dnes a zcela vážně v boji proti základům současné matematiky, zřejmě si nevšiml, že od dob antických klasiků uplynulo více než dva tisíce let a lidstvo je trochu někde jinde. Že Achilles dávno dohonil svoji želvu a Zénonův šíp dávno dopadl. Měli by si otevřít nějakou kvalitní středoškolskou učebnici a přečíst si definici limity a spojitosti…

Jako středoškolský student z toho vyvozuji: To znamená, pane učiteli (paní učitelko), že na přímce existují „místa“, kde není žádný bod. A v rovině jsou „místa“, kterým nelze přiřadit souřadnice (jakožto prvky množiny R2). A táži se: Můžete mi prosím nějaké takové „místo“ ukázat?

Pane učiteli (paní učitelko), ale k sestrojení kružnice či přímky je přece potřeba nejdříve znát alespoň dva body. Jak tedy sestrojím první přímku či kružnici, jestliže se tyto křivky mají narodit dřív než jakýkoliv bod? Co bylo dřív – slepice, anebo vejce?

Ano, jestliže na auto namontujeme nosič jízdních kol, získáme auto, na kterém můžeme převážet jízdní kola. Pro tuto schopnost ovšem auto nepřestane být autem. Ano, jestliže na množině definujeme metriku, získáme množinu, ve které můžeme měřit. Pro tuto schopnost ovšem množina nepřestane být množinou.

Vážení autoři, myslíte-li opravdu vážně to, co jsem z vašeho článku právě vytrhl, pak jste popřeli značnou část svého vlastního textu. Na jeho jiných místech totiž říkáte:

Takže, vážený pane učiteli (vážená paní učitelko), jak je možné, že přirozená, racionální či reálná čísla redukovat na množinu lze? I zde je přece potřeba uvést například vlastnosti operací s těmito čísly. Navíc třeba uspořádání, u přirozených čísel dále sudost, lichost, rozklady modulo libovolné přirozené číslo kromě jedničky, rozklad na prvočísla a čísla složená, trojúhelníková a netrojúhelníková, čtvercová a nečtvercová, abundantní a deficientní a bůhví, jaká ještě. Proč to všechno tedy neuvádíte a přirozená čísla, strukturu daleko bohatší než Gaussova rovina, redukujete na množinu, což je podle vašich vlastních slov zcela nesprávné?

Prostým obrazem množiny může být ovšem opět jenom množina. Ergo – číselná osa není přímka, protože, jak řečeno o tři ústřižky výše, přímku na množinu redukovat nelze.
Existenci prostého zobrazení mezi úsečkou a přímkou komentují Kuřina & Vondrová takto: “Toto tvrzení zdánlivě odporuje Eukleidovu axiomu 3: Celek je větší než díl.“ Geometrické útvary chápou autoři metricky a vadný axiom interpretují takto: „Přímka je delší než jakákoliv úsečka, která je její částí.“ Takže Eukleidés měl pravdu. Celek je vždycky větší než jeho díl a nějaká prostá zobrazení a množiny vůbec jsou jen moderním nesmyslem.
Převtělen do středoškolského studenta namítám: Ale pane učiteli (paní učitelko), ani nemnožinová přímka přece tento postulát nesplňuje. Ani pak přímka jako celek přece není větší než její díl – dílem přímky je třeba polopřímka. Celek a díl jsou i v tomto případě stejně dlouhé. Vždyť délka obou útvarů je nekonečná …
Obrázek v závěru článku…
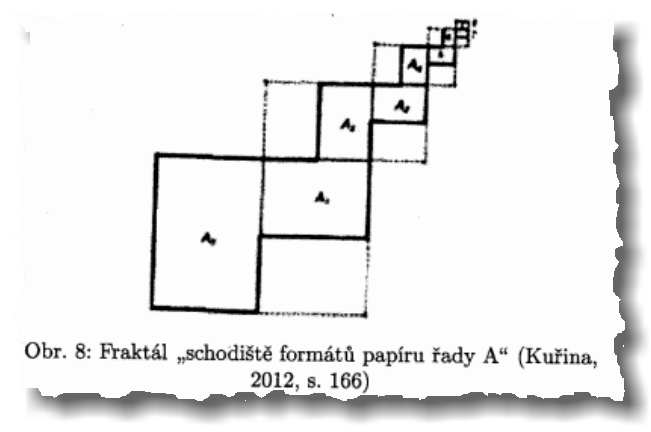
…je už jen prapodivnou třešničkou na věru nepodařeném dortu. Autoři citují klasika a zakladatele fraktální geometrie B. Mandelbrota: „Fraktály jsou tvary, u nichž – nezávisle na smyslu, který těmto slovům dáváme – detail reprodukuje část a část reprodukuje celek“
Nejen matematik, ale asi každý poznal, že tato slova nejsou definicí fraktálu, ale pouhou jeho elegantní zjednodušenou konturou. Návnadou, která má nalákat čtenáře k dalšímu čtení (jsou to slova z úvodu cca pětisetstránkové knihy). Kuřina s Vondrovou si nejenže nedali práci s vyhledáním korektní definice, ale ani velmi zjednodušenou charakteristiku, kterou citují, zjevně nepochopili.
Dejme tedy naposled slovo hypotetickému studentovi: Pane učiteli (paní učitelko), část vašeho schodiště z papírů jsem zakroužkoval a zvětšil:
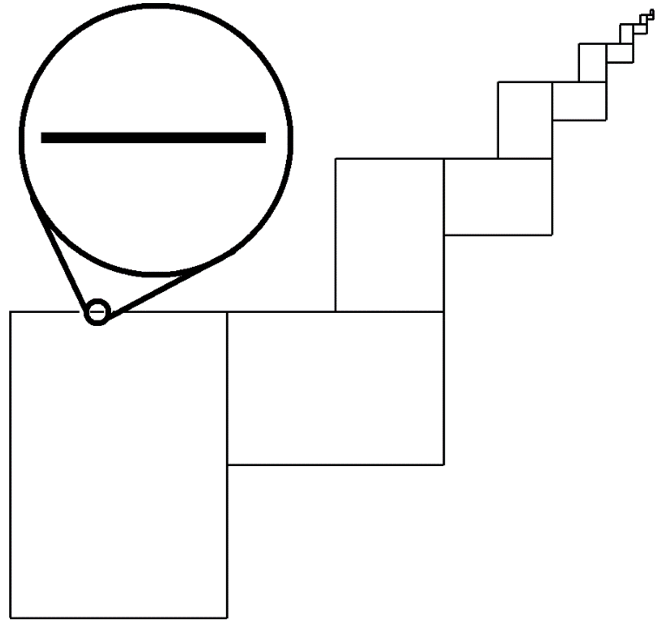
Můžete mi prosím říct, jak mám – byť nezávisle na smyslu – rozumět tomu, že tato část „reprodukuje celek“? Odpověď je jednoduchá – nijak. Po nějakém smyslu můžeš, milý studente, pátrat, jak chceš, tato část celek rozhodně nereprodukuje. Tento útvar totiž žádným fraktálem není. Chceš-li alespoň přibližně porozumět tomu, co fraktál je a co to znamená, když „část reprodukuje celek“, podívej se sem
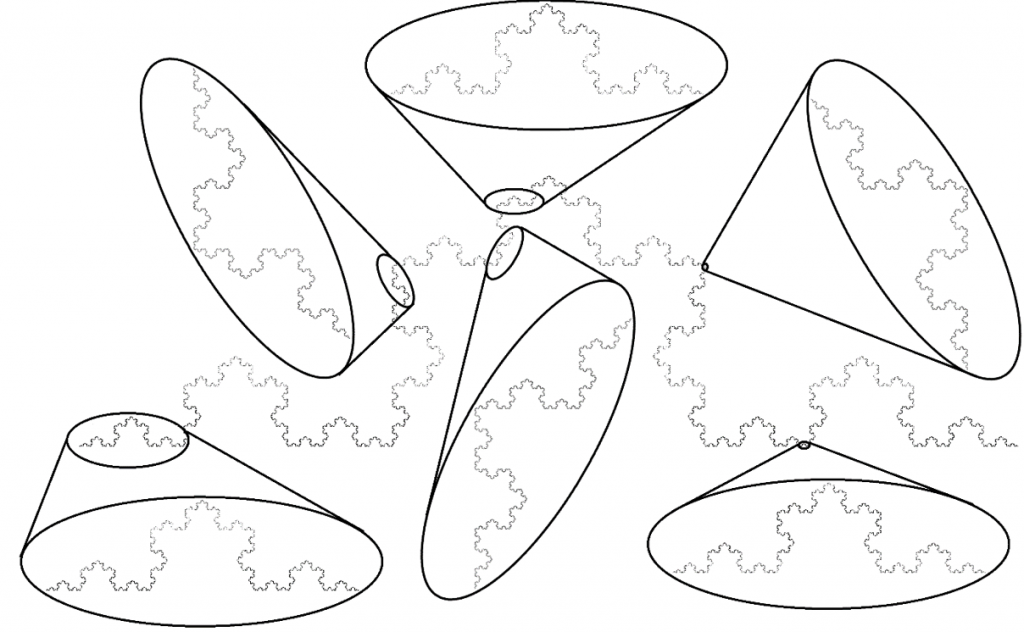
Takový obrázek však K&V nemohli nikde opsat ani odnikud převzít, a tak ho v článku nenajdeme.

Ale to je přeci v pořádku! To, že se představy žáků (nejen) o matematice mění, je přirozené a žádoucí! Nebo si snad autoři článku myslí, že třeťák uvažuje stejně jako oktaván? A všichni bez rozdílu věku bychom kvůli tomuto fatálnímu omylu měli moderní matematiku a dva tisíce let pokroku zahodit a vrátit se v čase zpět k Aristotelovi a Eukleidovi? Obávám se, že právě k tomu chtěli autoři této filipiky proti současné matematice učitele navádět.
==========================================
Epilog:
“Až dnes večer vzplanou hranice, ať jejich plameny očistí srdce každého z nás. Ať se vrátíme k tomu, co bylo a vždy by mělo být úkolem tohoto opatství – uchování lidského vědění. Říkám uchování, nikoli hledání! Neboť v dějinách vědění neexistuje žádný pokrok, nýbrž jen neustálé vznešené opakování.“
Ctihodný Jorge, severní Itálie léta páně 1327. Jméno kláštera Umberto Eco zamlčel.