Matematická úloha u přijímaček nebo v maturitních testech. Na jedné straně požadavek precizního zadání a jednoznačného výsledku, který má minimalizovat možnosti odvolávání a soudních tahanic. Na straně druhé široká propagace tzv. “logických řad”. Naprosto nejasných, s mnoha možnými výklady a výsledky, které k soudním dohrám přímo vybízejí.
Co to ta “logická řada” vlastně je?
Přiznám se, že nevím.
“Když něco nevím, tak se zeptám,” radí pan Horníček v jedné ze slavných předscén panu Werichovi. A tak jsem se zeptal i já. Strýčka Googla.
“Číselné a logické řady jsou řady čísel nebo znaků (případně jejich kombinace), které se rozvíjí podle určitého logického principu. Tento princip je předem neznámý a řešitel ho musí najít”, odpověděl strýček zde.
Jak určit “určitý logický princip”?
O tom, jak má být onen “určitý logický princip” určen, nikde ani slovo. A tak jsem si jako příklad vzal MF DNES, která umění doplňovat tyto řady považuje za “obecnou matematickou znalost”. Znalost zásadní až do té míry, že má být součástí přijímaček na střední školy:

Redakce zde zveřejnila přijímačkový test, který připravila agentura tutor, kde je (kromě jiných) tato úloha: Čísla tvoří logickou řadu. Doplňte chybějící členy:
121 144 ? 196 ? 256
Za odpověď 169 a 225 získáte tři body. Odpovíte-li jinak, máte smůlu a na gympl se kvůli tomu možná nedostanete. Ale proč? Jednoduše proto, že jste neuhodli duševní pochody zadavatele. S logikou a jejími principy to nemá co dělat. Zadavatel prostě a jednoduše myslel na druhé mocniny po sobě jdoucích přirozených čísel. Ostatní myšlenky jsou popraveny.
Já bych například doplnil něco úplně jiného: 69 a 9. Proč? Jednoduše proto:
Je snad součet horším “logickým principem”, než druhá mocnina? Pokud ano, tak proč? Já to nevím a neví to ostatně ani web matematika.cz, který stálý součet dvojic čísel přímo uvádí, jako možné řešení logické řady (viz https://matematika.cz/ciselne-rady odst. Další typy řad).
Čím dál tím hůř
A co sem?
2 4 10 28 ?
Podle serveru matematika.cz patří místo otazníku číslo 82. Proč? Inu proto, že 3*2-2=4; 3*4-2=10; 3*10-2=28 a konečně 3*28-2 je těch 82. Podle mě tam patří 62. Proč? Inu:

Aj tak možno. Alebo nie?
Je tento můj duševní pochod horší nebo méněcenný? Pokud ano, tak proč? A čtenář nejspíš vymyslí a zdůvodní další čísla, která tam patří podle úplně jiných “logických principů”. Ale u zkoušky by měly všechny naše myšlenky smůlu – bodovaný je jen duševní pochod autora příkladu.
Co sem?

Nevypadá to, že by jednotlivá čísla v řádcích či sloupcích tvořila nějaké “jednoduché” posloupnosti. Zkusme sčítat řádky: 15, 18, 21, ?, 27. Násobky tří? Pak by na místě otazníku v tabulce musela být třináctka. Zkusme s tou třináctkou sečíst sloupce: 16, 16, 30, 3, 40. Nic. Že by to tedy ta třináctka nebyla? Řešitel znejistí, obrátí noviny a podívá se na “správné ” řešení – opravdu 13. Zadavatel úlohy zřejmě neměl na to, aby vymyslel “magičtější” čtverec. Ona to taky u čtverce s pětadvaceti čísly není žádná legrace.
U skutečné zkoušky ovšem uchazeč noviny obracet nebude a nejspíš bude hledat dál. Může třeba sečíst řádky a sloupce s tím, že pole s otazníkem je prázdné. Dostane 15, 18, 21, 11, 27 a 16, 3, 30, 3, 40. Násobky jsou, pravda, pryč, ale je tu jiná zajímavá věc: sečte-li nyní tyto dvě pětice čísel, dostane v obou případech číslo 92 – to je přece výsledek jako hrom! Takže co patří místo otazníku? Nula!! A součet součtů řádků je roven součtu součtů sloupců.
Bude-li mít sílu ještě chvíli myslet, zjistí, že tato rovnost zůstane zachována, i když na místo otazníku napíše nabízenou desítku. I patnáctku. A devítku. A dokonce jakékoliv jiné číslo. Máme zde “logický princip”, podle kterého můžete doplnit číslo, jaké chcete. Vyhovují mu úplně všechna. Dokonce i ta komplexní. Prostý důsledek komutativního a asociativního zákona, který se často používá právě na kontrolu součtů v takových tabulkách. Jenže tento objev vám může paradoxně cestu k dalšímu vzdělávání zavřít. Žádné body za něj totiž nejsou.
Co toto?
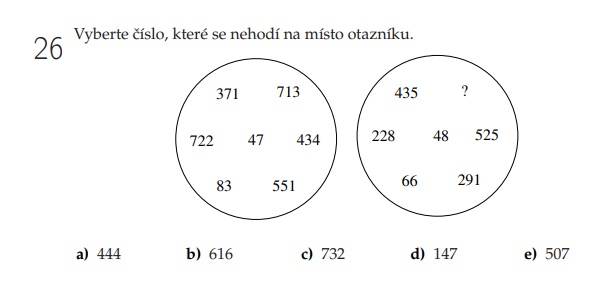
Všimli jste si, že všech sedm čísel v prvním kruhu dá po vydělení třemi zbytek dvě, kdežto všech šest čísel v pravém kruhu je třemi dělitelné beze zbytku? A že pro čtyři nabízená čísla platí totéž, zatímco pro číslo b) nikoliv? Gratulují! Uhodli jste duševní pochod autora úlohy a máte bod. Já jsem si bohužel daleko dřív všiml, že žádné číslo ani v kruzích ani v možnostech není zapsáno třemi stejnými číslicemi – kromě jediného, které tam tedy nepatří. Jenže to je a), takže tento můj duševní pochod bodovat nebude…
Moc myslet se dnes nevyplácí
Příklad 26 se dvěma kruhy čísel dělitelných či nedělitelných třemi se opakoval ve všech dvanácti variantách testů MU v roce 2011. A nejen v něm. V jiných letech byla čísla skrývající tento “logický princip” v různě lomených čarách, hadech a bůhví čem. Jednoduchá rada “podívej se na ciferný součet dvou-tří čísel a je jasno” slavila úspěch v celkem sto patnácti úlohách během cca pěti let. Další stovky podobných úloh v deseti posledních letech omílaly n2 podobně, jako první dnes uvedený příklad. Objevil jsem ještě stovky 2n+1 a stovky 2n-1.
Spousta lidí si draze platí několikaměsíční přípravné kurzy různých více či méně pochybných agentur, které nejsou ničím jiným, než rozvleklým rádoby tréninkem na podobné “testy studijních předpokladů”. Já mám pro každého, koho takový test čeká, jednoduchou radu: “Hledej ciferný součet, tři vzorečky a číslice či písmenka si rozděl na hranatá a kulatá. Každé jiné myšlení škodí.” Tato zásada zvedla v minulosti několika lidem předpoklady pro studium na Masarykově univerzitě o deset až patnáct procent. Zadarmo a během dvou minut.
Propagace matematicky vadných postupů
“Společný jmenovatel” všech výše uvedených “logických principů” má přesný název – je to tzv. neúplná indukce. Může vést k zajímavým objevům a podobné příklady jsou asi dobrým intelektuálním tréninkem. Na druhé straně je tento “princip” zcela subjektivní záležitostí. Může vést k zásadním omylům, proto nepatří do matematiky. Z hlediska matematiky je dokonce vadný. Vede k různým výsledkům, a proto zcela jistě nepatří do žádných zkoušek, tím méně do testů rozhodujících o něčí budoucnosti.
Chápu, že se všichni musíme nějak živit, ale to, co se dnes děje kolem přijímaček na střední či vysoké školy, hraničí podle mě s ohrožováním výchovy mládeže.